Computational Biology
分子力场
键长伸缩项
描述键长$b_i$在平衡位置$b_{i,0}$附近振动的能量。$k_i$为键伸缩力常数,可由实验测得的键振动频率计算得:$\nu = \frac{1}{2\pi}\sqrt{k_i/M}$ ,其中$M=m_1m_2/(m_1+m_2)$
键角弯曲项
描述键角$\theta_i$在平衡位置$\theta_{i,0}$附近振动的能量。$k_i$为键伸缩力常数。
二面角扭转项
𝑉𝑛为二面角扭转势常数,表示旋转能垒的高度;整数𝑛表示多重性,即绕键旋转360°时出现的能量最小值的次数;$\phi$为二面角;$\delta$为相位因子,其通常取0或者$\pi$,用来决定cos项的正负符号。
范德瓦尔斯作用项(Lennard-Jones势能)
这是一个经验方程。式中的$r_{i,j}$表示原子对(i,j)之间的距离。
$\epsilon$和$\sigma$为势能参数,随原子对的种类而异。$\epsilon _{i,j}=\sqrt{\epsilon_i\epsilon_j}$, $\sigma_{i,j}=\frac{1}{2}(\sigma_i+\sigma_j)$
静电相互作用项(Coulomb势能)
$\epsilon_0$为真空介电常数。
能量最小化
能量最小化相当于求解势能函数的全局极小值过程,其中势能函数是多个独立变量的函数$f(x_1,x_2,…,x_n)$,极小值条件为:
最速下降法
设向量$g_k$为势能函数在分子位于构象$X_k$(为一个坐标)时的梯度(能量的梯度是力),即
迭代一次后的构象坐标为
$\lambda$表示步长
共轭梯度法
当前值和目标值之间具有残差,用当前的梯度构建一个和残差正交的向量
每次走的方向恰好是与残差正交的,这意味着:每走一步恰好能消除残差的一个方向,当消除了残差所有投影方向上的值,那么就消除了整个残差。当势能函数是m个变量的函数时,经过m步就能达到目标值。
牛顿-拉森法
首先从泰勒级数展开开始讨论,$f(x)$在点$x_k$处的泰勒级数展开为:
保留前三项,进行一次求导
在极小值点$x=x^*$处,函数的一阶导数为0
对于多元函数体系,也可得到类似的关系式:
其中$(\boldsymbol{f}’’)^{-1}(\boldsymbol{X}_k)$为原函数二阶导数组成的Hessian矩阵的逆矩阵
收敛判据
- 能量误差:$\Delta U = U_n - U_{n-1} < \epsilon$ 时停止计算
- 坐标移动:$\Delta x_n^2 = |x_n|-x_{n-1}^2 < \epsilon$ 时停止计算
- 梯度均方根误差:$RMS = \sqrt{\frac{g^Tg}{3N}}< \epsilon$ 时停止计算
分子动力学模拟
采用有限差分法,即用有限的时间间隔$\Delta t$取代无穷小的$dt$,然后通过数值积分方法完成运动方程的求解。
分子运动方程及其数值求解
对于某个粒子i,描述其运动的方程(速度与位移矢量)为:
数值求解:速度Verlet算法
先由当前速度和力得到新的位置和半时间速度,再由新的位置得到新的力,结合半时间速度更新得到新的速度。
刚性分子运动的处理
将分子中原子的相对位置固定,分子内无仍和键长或键角的变化。水分子长采用这种运动模型。
质心平动
整个分子处理为单个粒子,由作用于其上的合力决定
质心定义为:
n为分子中原子总数,$m_i$和$\boldsymbol{r_i}$为每个原子的质量和位置矢量,M为分子总质量。
质心转动
b表示分子固定坐标轴,s表示空间固定坐标轴。定义欧拉角$\phi,\Psi,\theta$, 则两个坐标系中坐标变换的关系为:
A为旋转矩阵:
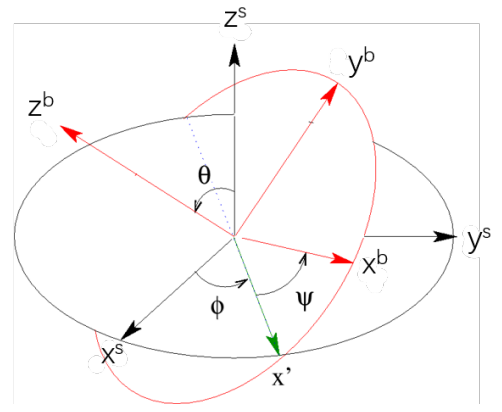
为减小数值计算的误差,定义4分量矢量$\mathbf{Q}=(q_0,q_1,q_2,q_3)$,且$|\mathbf{Q}|^2=1$,且该矢量与欧拉角之间有如下关系:
可以推导出分子固定轴坐标系中的角速度方程组,可以用数值方法求解:
利用四分量形式改写后的旋转矩阵,可以求解空间固定轴中的角速度:
周期性边界条件
在无限空间里复制有限大小的模拟盒子(simulation box),从而尽可能地体现真实研究环境。在周期性边界条件下,当体系中任一粒子移出模拟盒子外,则必有一粒子由相对的方向移入。这样的限制条件能够保持系统中的粒子数目恒定,密度不变,符合实际的要求。立方(cube)格子是最简单也最常见的周期体系。举例来说,对于一个球形分子选择立方格子不是最合适的,而选择缺角八面体或者菱形十二面体可能会更好一些,因为后者包含的溶剂分子(如水分子)数目要小,更利于计算。
一方面,模拟盒子不能太大,以免引入过多的溶剂分子,影响体系计算效率;另一方面,模拟盒子也不能太小,需要避免所谓的有限尺寸效应(finite-size effects)。在对生化分子如蛋白质、核酸模拟时,分子表面距离任一边界的距离不小于10埃是一个常用来指导模拟盒子大小选择的参考。
短程相互作用力处理
截断半径法
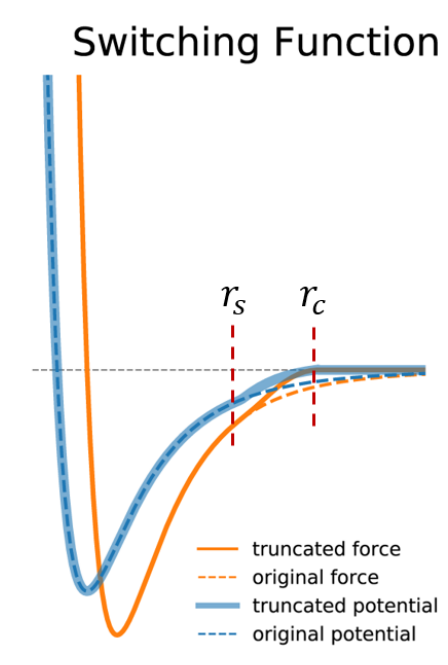
引入一个开关函数$S(r)$,当两个粒子之间的距离大于开关半径,即$r>r_s$时,触发开关函数,调整相互作用力快速到达0,当两个粒子之间的距离大于截断半径,即$r>r_c$时,相互作用力归零。
其中$S(r)$为:
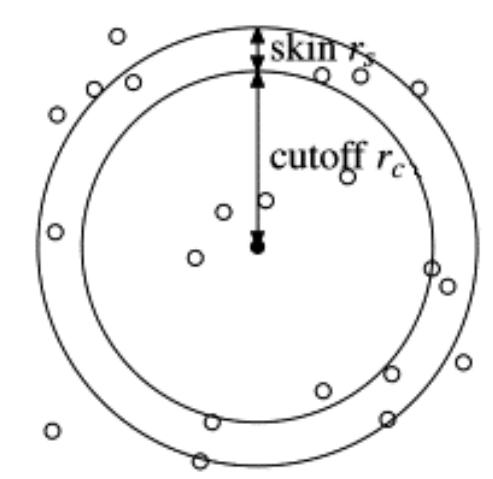
邻近列表法
近邻列表方法的基本思想是为体系中的每个粒子构建并维护一个近邻列表。在模拟过程中,近邻列表将以固定的时间间隔定期更新,或者当某些粒子的位移超出某个预设值时自动更新。当为粒子i构建近邻列表时,如果其与另一个粒子j之间的距离$r_{ij}\le r_c+r_s$时,则将它们视为“相邻” 。其中$r_c$为截断半径,额外“皮肤”距离$r_s$用来把稍大于截断距离的一些粒子也包含进来。需要注意的是,额外“皮肤”距离$r_S$应该足够的大,以便在两次近邻列表重建的间隔内,如果一个粒子A预先不在另一个粒子B的近邻列表中,则A粒子不可能穿透B粒子的”皮肤“进入其截断半径范围内。
近邻列表的适时更新非常重要。如果更新频率太快,那么这个过程就不会起到应有的效果;而更新太慢,则会影响体系能量和作用力的正确计算。在实际模拟过程中,人们普遍认可的更新频率为10~20步。此外,需要说明的是,对额外“皮肤”距离$r_s$值的选取并没有一成不变的规则,但其与列表更新频率之间存在一种平衡:如果更新频率越小,则额外“皮肤”距离$r_s$就越大;反之亦然。一般地,在分子动力学模拟中采用近邻列表方法可大幅度地降低计算时间.
长程相互作用力处理
Edwald求和法
在这种方法中,每个粒子都要与模拟盒子中的其他粒子及周期性镜像格子中的所有粒子发生相互作用。首先,我们考虑边长为L的立方模拟盒子,其中含有N个带电粒子,从而中心模拟盒子中的静电相互作用可写成:
然后我们考虑中心模拟盒子的最近邻镜像格子。在三维空间中,中心盒子会有6个相距为L的最近邻镜像格子,因而中心盒子里的粒子与六个近邻镜像格子中所有粒子之间的静电相互作用可表示为:
进一步地,我们可以不断重复罗列周期性镜像格子(以球形的方式),从而得到中心盒子中粒子与其他所有周期性镜像格子中粒子间的静电相互作用:
其中$\vec{n}=(n_xL,n_yL,n_zL)$,$n_x,n_y,n_z$为整数。
但实际计算中,上述函数收敛极慢,计算技巧是将上式转换成两个收敛得更快的级数来计算:
因此,我们的目标变为选择一个合适的函数f(r),该函数将处理r较小时随1/r的快速变化和较大r时的缓慢衰减。
为了寻找f(r),可以想象每一个带电粒子都被由等量但符号相反的可中和的电荷(这种电荷在空间上满足高斯分布)所包围,那么体系总的静电相互作用等于带电粒子间的相互作用加上中和电荷分布间的相互作用。此时静电相互作用可以表示为:
式中,$erfc(x)$ 为补余误差函数,其表达式为:
为了抵消中和电荷,又要引入新的电荷,其产生的静电相互作用可以表示为:
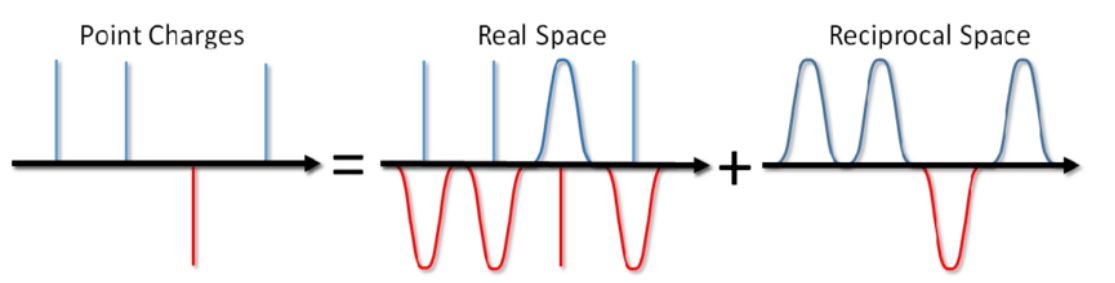
Edwald求和的总体效果就是将点电荷转化为符合高斯分布的电荷,再通过网格采样变为离散的值,从而可以进行快速傅里叶变换来提升计算速度。